Exercices corrigés - Homothésies - 3e
Consultez gratuitement des exercices sur les homothésies de 3e de collège avec les corrigés détaillés en PDF ou en ligne.
Exercice 1
Difficulté : 40/100
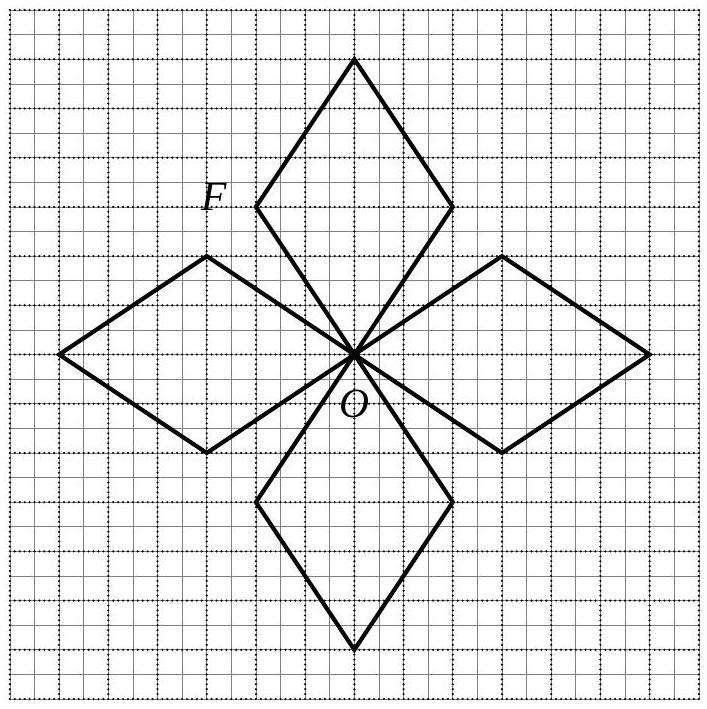
Construire l’image \(F^{\prime}\) de la figure \(F\) par une homothétie de centre \(O\) et de rapport \(+2\).
Exercice 2
Difficulté : 50/100
Question : Un triangle \(DEF\) rectangle en \(D\) et d’aire \(24 \, \mathrm{cm}^{2}\) est un agrandissement d’un triangle \(XYZ\), rectangle en \(X\), tel que \(XY = 4 \, \mathrm{cm}\) et \(XZ = 3 \, \mathrm{cm}\). Calcule les longueurs \(DE\) et \(DF\).
Exercice 3
Difficulté : 40/100
La pyramide de la Place de la Concorde est une pyramide régulière à base carrée de 50 m de côté et de 30 m de hauteur.
Fais un schéma.
Calcule le volume \(\mathcal{V}\) de cette pyramide. Donne la valeur exacte en \(\mathrm{m}^{3}\), puis la valeur arrondie à l’unité.
Sur une maquette, on construit une réduction de cette pyramide. Le côté de la base carrée mesure 10 cm. Calcule le coefficient de réduction.
Déduis-en le volume \(\vartheta^{\prime}\) de la pyramide sur la maquette. Donne la valeur exacte en \(\mathrm{cm}^{3}\), puis la valeur arrondie à l’unité.
Exercice 4
Difficulté : 50/100
Question :
- Construis un triangle dont les côtés mesurent \(6\,\text{cm}\), \(7\,\text{cm}\) et \(10\,\text{cm}\). Réalise un agrandissement de ce triangle de manière à ce que le côté de \(7\,\text{cm}\) mesure désormais \(14\,\text{cm}\).
Mesure les angles de chaque triangle. Que constates-tu ?
Construis deux triangles \(DEF\) et \(D'E'F'\), de tailles différentes, dont les angles mesurent : \[ \widehat{EDF} = \widehat{D'E'F'} = 65^\circ,\quad \widehat{DFE} = \widehat{D'F'E'} = 55^\circ,\quad \widehat{FED} = \widehat{F'E'D'} = 60^\circ \] Mesure les côtés de ces triangles, puis calcule les rapports suivants : \[ \frac{DE}{EF},\quad \frac{DE}{DF},\quad \frac{EF}{DF},\quad \frac{D'E'}{E'F'},\quad \frac{D'E'}{D'F'},\quad \frac{E'F'}{D'F'} \] Que constates-tu ?
Fais de même pour les rapports suivants : \[ \frac{DE}{D'E'},\quad \frac{EF}{E'F'},\quad \frac{DF}{D'F'} \]
Exercice 5
Difficulté : 50/100
Question :
Construis l’image de la figure représentée sur la figure par la transformation \(\mathfrak{H}\left(C ; \frac{2}{3}\right)\).
Construis ensuite l’image de la figure obtenue en a) par la transformation \(S(d)\).
Comment peut-on revenir à la figure initiale à partir de la figure obtenue en b) ?
Exercice 6
Difficulté : 40/100
Question : Les côtés du triangle \(XYZ\) mesurent respectivement \(7\) cm, \(10\) cm et \(14\) cm.
Sophie décide de tracer à la craie un agrandissement de ce triangle.
Elle choisit alors des longueurs de côtés de \(21\) cm, \(30\) cm et \(42\) cm.
Son agrandissement est-il correct ?
Exercice 7
Difficulté : 50/100
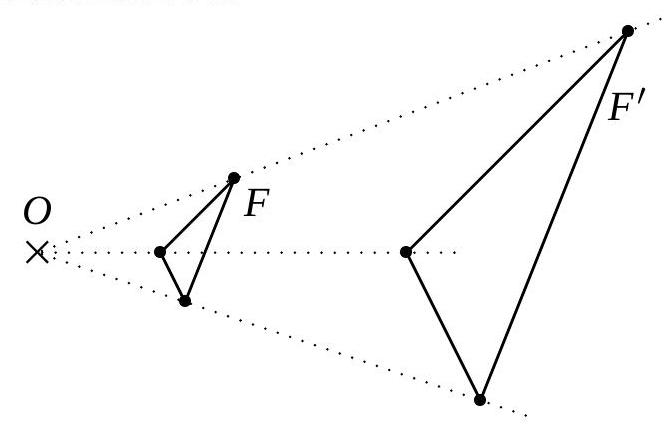
Soit \(F^{\prime}\) l’image de \(F\) par une homothétie.
- Effectuez les mesures nécessaires afin de calculer le rapport de l’homothétie.
- Quel est le rapport de l’homothétie qui transforme \(F^{\prime}\) en \(F\) ?
Exercice 8
Difficulté : 50/100
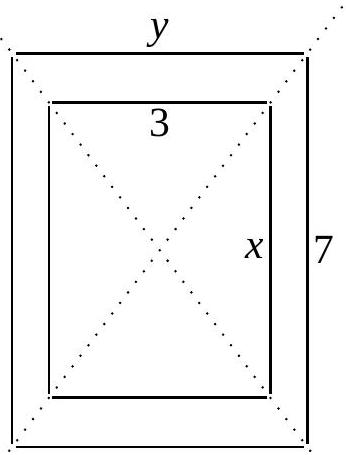
Voici un rectangle et son image par une homothétie de rapport \(\frac{4}{3}\). Calculez les longueurs \(x\) et \(y\).
Unité : cm
Exercice 9
Difficulté : 40/100
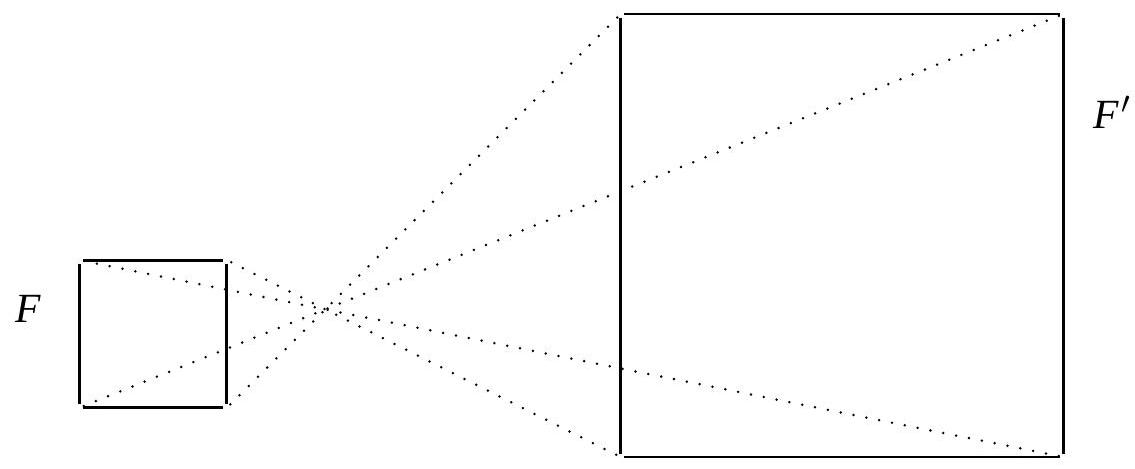
\(F^{\prime}\) est l’image de \(F\) par une homothétie.
- Effectuez les mesures nécessaires et calculez le rapport d’homothétie.
- Calculez l’aire du carré \(F^{\prime}\) et l’aire du carré \(F\).
- Calculez le rapport de ces aires.
Exercice 10
Difficulté : 50/100
L’homothétie de centre \(M\) et de rapport \(\frac{3}{2}\) transforme un segment \([CD]\) en un segment \([C'D']\).
Construis cette figure.
Que peut-on dire des droites \((CD)\) et \((C'D')\) ? Justifie.
Exercice 11
Difficulté : 40/100
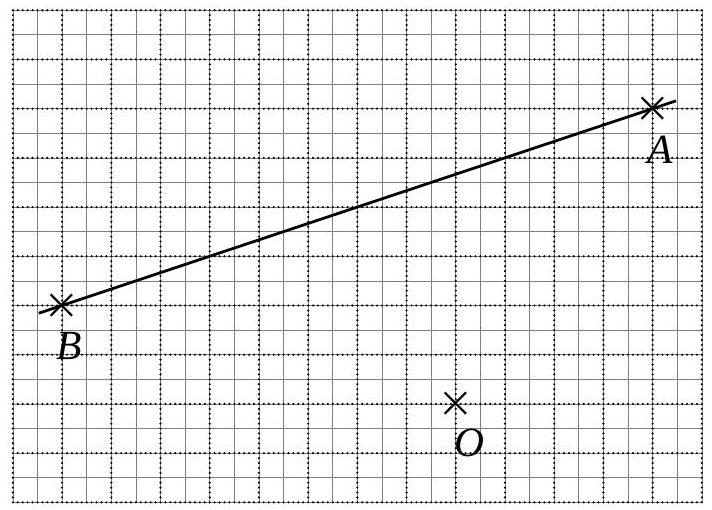
Construire l’image de la droite \(d\) par une homothétie de centre \(O\) et de rapport \(\frac{1}{2}\).
Construire l’image de la droite \(d\) par une homothétie de centre \(O\) et de rapport \(-\frac{1}{2}\).
Construire l’image de la droite \(d\) par une homothétie de centre \(O\) et de rapport \(5\).
Exercice 12
Difficulté : 20/100
Question : Un triangle \(D'E'F'\) est l’image du triangle \(DEF\) par une homothétie de rapport \(\frac{3}{2}\). On sait que \(DE = 8\,\mathrm{cm}\) et que l’angle \(\widehat{DEF}\) mesure \(45^\circ\). Déterminez les mesures de \(D'E'\) et du périmètre de \(D'E'F'\). Justifiez votre réponse.
Exercice 13
Difficulté : 45/100
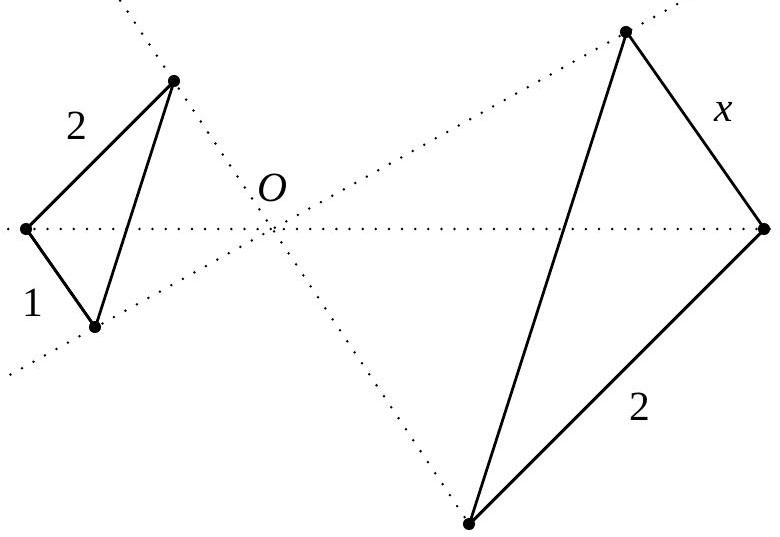
Calculer le rapport d’homothétie et la longueur du segment \(x\).
Unité : le cm
Exercice 14
Difficulté : 35/100
Question : Une figure a une aire de \(94\ \mathrm{cm}^2\). Après une réduction, on obtient une nouvelle figure dont l’aire est de \(67,35\ \mathrm{cm}^2\). Détermine le rapport de réduction.
Exercice 15
Difficulté : 50/100
Question : Trace le rectangle \(EFGH\) et place un point \(P\) à l’extérieur. Construis \(E'F'G'H'\), l’image du quadrilatère \(EFGH\) par homothétie de centre \(P\) et de rapport \(1{,}5\).
Exercice 16
Difficulté : 30/100
Question :
- Complète le tableau suivant.
| Aire de la figure | Rapport d’homothétie | Aire de l’image |
|---|---|---|
| \(4 \, \mathrm{cm}^{2}\) | 2 | |
| \(18 \, \mathrm{m}^{2}\) | 0,5 | |
| 3 | \(243 \, \mathrm{mm}^{2}\) | |
| 0,4 | \(1{,}44 \, \mathrm{cm}^{2}\) | |
| \(3{,}0 \, \mathrm{cm}^{2}\) | \(12 \, \mathrm{cm}^{2}\) | |
| \(3 \, \mathrm{dm}^{2}\) | \(3{,}24 \, \mathrm{dm}^{2}\) | |
| \(12 \, \mathrm{dm}^{2}\) | \(12 \, \mathrm{m}^{2}\) |
- Complète l’équation suivante.
\[ \frac{\text{Aire IJKL}}{\text{Aire WXYZ}} = (\ )^{2} \]
Exercice 17
Difficulté : 40/100
Question : L’aire d’un hexagone est de \(30\,\text{cm}^2\). Déterminez l’aire de son image par une homothétie de rapport :
\(1,5\) ;
\(-3\) ;
\(\dfrac{2}{5}\).
Exercice 18
Difficulté : 40/100
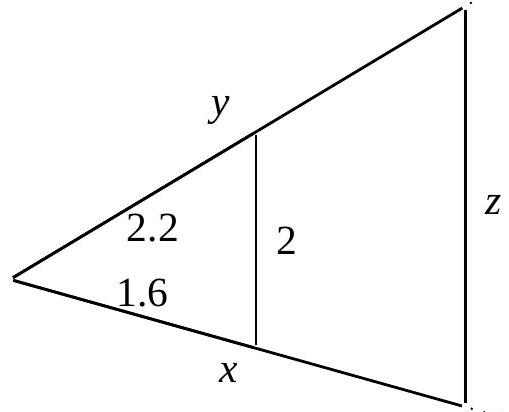
Voici un triangle et son image par une homothétie de rapport 1,85. Calculer les longueurs \(x\), \(y\) et \(z\).
Unité : le dm
Exercice 19
Difficulté : 50/100
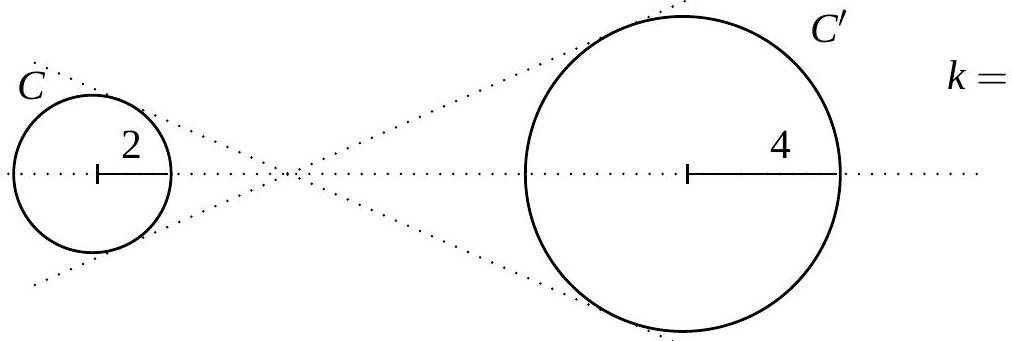
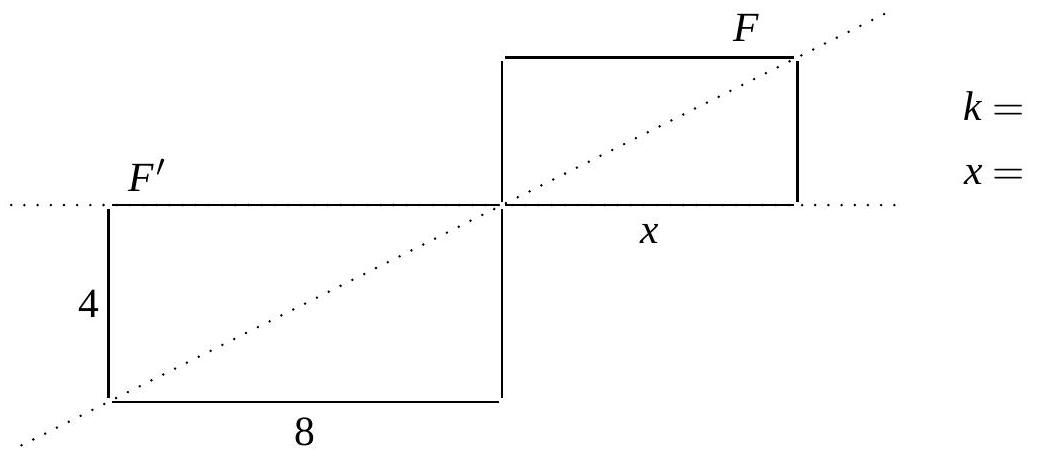
Voici plusieurs figures et leurs images par une homothétie. Pour chaque figure, indiquez le rapport d’homothétie \(k\). Pour les figures (a) et (d), déterminez également la longueur \(x\).
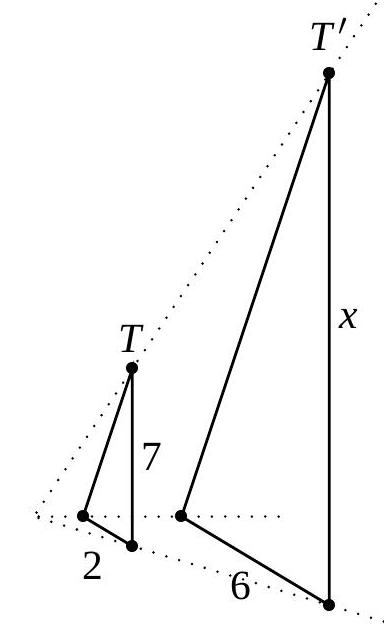\(k =\)
\(x =\)
\[
k =
\]
Exercice 20
Difficulté : 35/100
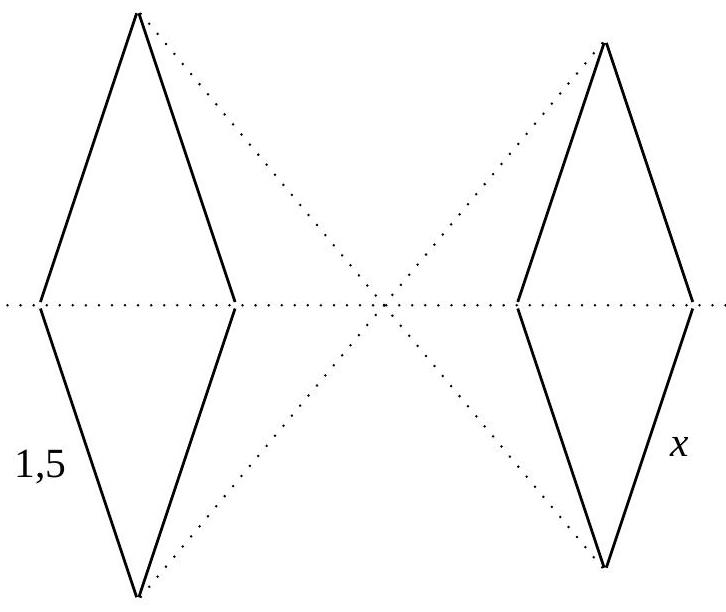
Voici un losange et son image par une homothétie de rapport \(-0{,}9\). Calculez la longueur \(x\). Unité : m.
Exercice 21
Difficulté : 35/100
Question : La figure \(M^{\prime}N^{\prime}O^{\prime}P^{\prime}\) est l’image de la figure \(MNOP\) par homothétie de ce centre et de rapport 2. Quelles sont les dimensions de \(M^{\prime}N^{\prime}O^{\prime}P^{\prime}\) ?
Exercice 22
Difficulté : 40/100
Deux triangles ont les longueurs suivantes.
| Triangle ABC | \(\mathrm{AB}=6,0\) | \(\mathrm{AC}=9,0\) | \(\mathrm{BC}=12,0\) |
|---|---|---|---|
| Triangle DEF | \(\mathrm{DE}=3,0\) | \(\mathrm{DF}=4,5\) | \(\mathrm{EF}=6,0\) |
Est-ce un tableau de proportionnalité ? Justifie.
Le triangle ABC est-il un agrandissement ou une réduction du triangle DEF ? Précise le rapport.
Exercice 23
Difficulté : 20/100
Question : Le carré \(IJKL\) est l’image du carré \(WXYZ\) par une homothétie de rapport 4. On suppose que le côté du carré \(WXYZ\) mesure 2 cm.
- Calcule la longueur d’un côté de \(IJKL\) et en déduis son aire.
Exercice 24
Difficulté : 50/100
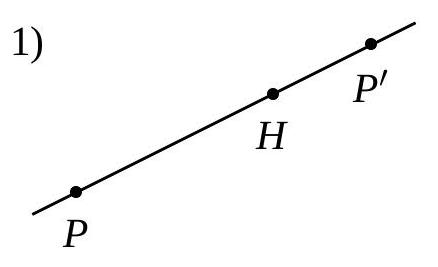
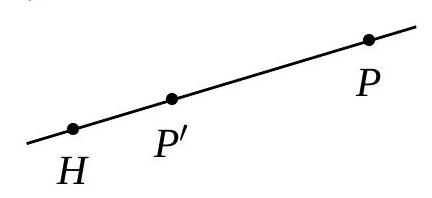
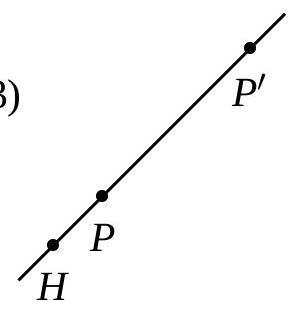
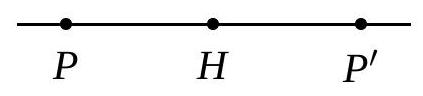
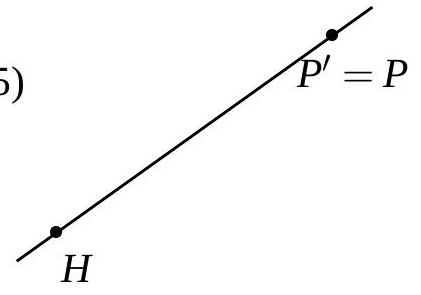
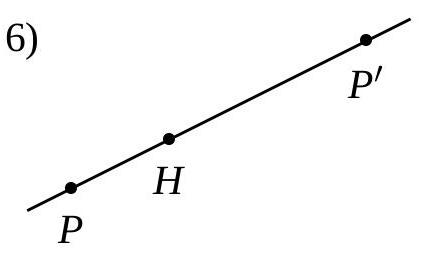
Dans chacune des figures suivantes, le point \(P^{\prime}\) est l’image du point \(P\) par une homothétie de centre \(H\). Pour chaque figure, indiquez :
- Si le rapport d’homothétie est positif ou négatif ;
- Si, en valeur absolue, le rapport est inférieur, égal ou supérieur à 1.
Exercice 25
Difficulté : 40/100
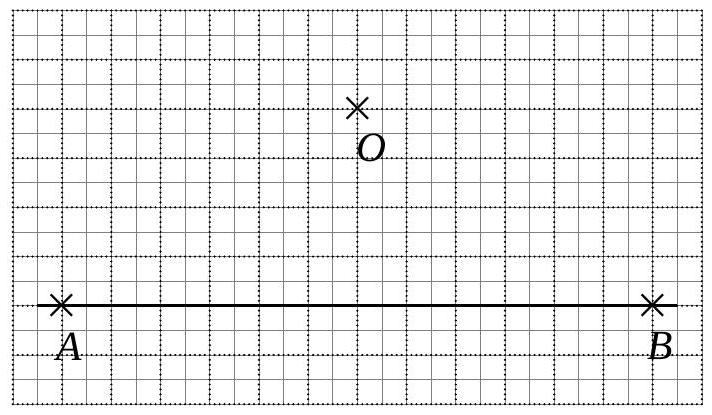
Construire l’image du segment [AB] par une homothétie de centre \(O\) et de rapport \(-\frac{1}{3}\).